K-D tree入门

K-D tree入门

九月 05, 2021

KNN问题

​ K-Nearest Neighbor，我也不知道应该说是问题还是算法，也就不要管这个了。我们想象这样一个场景，在一个平面直角坐标系上面，有很多很多个点。现在我们随机地选择一个点，想要知道离他最近的$k$个点是哪些，怎么办。如果使用肉眼观察的话，那么我们是可以大致判断出来有哪些的。可是在很多时候，我们拿到的并不是图像，而是数据，而这些数据要让计算机来处理，怎么办？？

​ 对于这一个问题，我们可以用时间复杂度为$\Theta(n^2)$的方法，处理出所有的距离，询问到处理的距离里面来看，但是我们还可以有别的方法。

K-D tree

概念

​ K-D tree 是一棵二叉查找树,它可以用来维护有多维信息的数据。因为在做题的时候，遇到的一般都是$2$维,所以说下面的例子我就以二维的来看了

建立

解释

​ 平常的二叉查找树，建立的时候，在每一个中间节点，会比较值的大小，比他小的就到他的左儿子那边，比他大的就到他的右儿子那边。但是K-D tree 有多维信息，这种情况下应该怎么办？既然他是有K维的信息，那么我们就任意选择其中以为来进行分割就可以了。这就好像是在平面中画了一条线一样，将它们分成了两个部分
​ 比如下面的这一个，这是一个这个平面上有很多点，我们先选取其中一维进行分割，分成了两块，然后我们换一维继续分割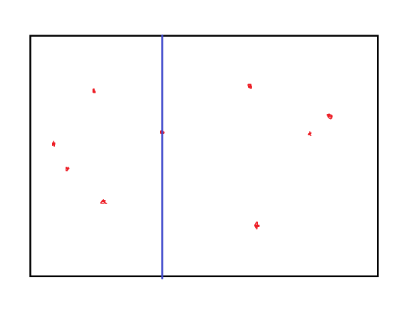
k1.png
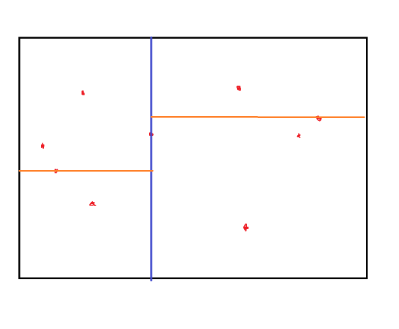
k2.png

​ 就这个样子交替分割下去就可以了，听着是不是就像切蛋糕一样？

​ 那么怎么来进行分割呢，有下面两种方法：

  • 根据深度，轮流来选择一个维度，依据这一个维度来进行划分。在划分的时候将区间内的值依照这一维的大小来进行排序，然后将中位数存下来，然后再递归的处理
  • 我们计算一下每一维的方差，然后选择方差最大的那一维来进行划分。为什么要这样来进行划分，举个例子，如果说是一块方方正正的豆腐，那么不无论选择那一维来切，效果都是很好的。但是呢，如果说是一根细长木条呢？你轮流切未必就有一个好效果。选择计算每一维的方差，选择方差最大的那一维来的话，能够在构建树上起到很好的效果。

(假)代码

首先，我们需要一个结构体

1
2
3
4
5
6
7
8
struct K_D_Tree{
	node d[maxn];
	int lc[maxn];
	int rc[maxn];
#define D(i,j) d[i].databank[j]
#define Minp(i,j) d[i].minpos[j]
#define Maxp(i,j) d[i].maxpos[j]
}

​ 其中$node$是用来储存信息的结构体，然后来看看第一种方法如何来进行$build$

1
2
3
4
5
6
7
8
9
10
11
int build(int L,int R,int deps){
		if(L>R)return 0;
		int mid=(L+R)>>1;
		keyd=deps%maxk;
		nth_element(point+L,point+mid,point+R+1);
		d[mid]=point[mid];
		lc[mid]=build(L,mid-1,deps+1);
		rc[mid]=build(mid+1,R,deps+1);
		pushup(mid);
		return mid;
	}

​ 这里$pushup$这个函数在接下来会讲，所以说先看着。nth_element 这一个函数第一个和第三个参量是左右区间，左闭右开，而中间的这一个则是你要排的值。像是上面代码中的那个例子，在point+mid这个位置，一定就是这个区间的中位数，前面都比它小，后面都比他大，但是前面后面未必就排好了序。

​ 第二种方法（假代码）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for(int i=0;i<maxk;i++){
	double aver=var[i]=0.0;
	for(int j=L;j<=R;j++)
		aver+=D(j,i);
		aver/=(R-L+1);
		for(int j=L;j<=R;j++){}
			var[i]+=((D(j,i)-aver)*(D(j,i)-aver));
		}//计算方差 
		dim[now]=0;
		for(int i=1;i<k;i++){
			if(var[dim[now]]<var[i])dim[now]=i; 
		} 
		 nth_element(……)
		 //还要记录一下维度,然后和上面一样递归处理就可以了

查询

K-D tree 的K近邻查询

​ 我们之前提到了，要查询离某一个节点第$k$远（当然也可能是第$k$近）的节点的编号，或者是这一个距离。首先，这个第$k$远怎么办，怎么来记录，这个时候就可以想到优先队列了，每一次询问的时候，我们在优先队列里面先$push$ k个值进去，然后呢，查询的时候，遇到符合要求的数值，就把队首$pop$出来，然后再$push$进去，这样就可以保证我们总是维护好了第$k$远或者第$k$近了。

​ 接下来来谈一谈如何查询，首先我们遍历到某一个节点，然后计算一下这一个节点和目标节点之间的距离，看看这一个距离是否符合要求，如果符合我们的要求，那么我们就更新一下，接着，以目标节点作为圆心，现在的答案的距离作为半径，然后做一个圆（三维的情况下是一个球，如果更多的话，那么就是超球体了）然后看看这一个圆有没有和我们遍历到的节点划分的左右平面(多维的话，按照网上的叫法就是超平面了)相交。如何判断？我们计算一下目标节点到左右平面的最小距离(注意，这里是在说第k近的情况)，如果说这个距离要比我们现在所说的这一个答案要小的话，那么就到这个平面里面去搜索，而如果是第k远的的情况下面，就是计算最远的距离是多少，然后再来判断了

​ 可是现在还有一个问题，怎么来确定离左右平面的距离？这个时候就可以记录下每一个节点的子树下面，某一维最大最小的值是多少，建立的时候$pushup$一下，计算的时候就可以用了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
struct node{
	double databank[2];
	double minpos[2];
	double maxpos[2];
	
	bool operator <(const node &cmp)const{
		return databank[keyd]<cmp.databank[keyd];
	}
}point[maxn]; 
struct K_D_Tree{
	node d[maxn];
	int lc[maxn];
	int rc[maxn];
#define D(i,j) d[i].databank[j]
#define Minp(i,j) d[i].minpos[j]
#define Maxp(i,j) d[i].maxpos[j]
	
	inline void pushup(int now){
		if(lc[now]){
			for(int i=0;i<maxk;i++){
				Minp(now,i)=min(Minp(now,i),Minp(lc[now],i));
				Maxp(now,i)=max(Maxp(now,i),Maxp(lc[now],i));
			}
		}
		if(rc[now]){
			for(int i=0;i<maxk;i++){
				Minp(now,i)=min(Minp(now,i),Minp(rc[now],i));
				Maxp(now,i)=max(Maxp(now,i),Maxp(rc[now],i));
			} 
		}
	}	
};

​ 如果是计算最远的距离的话，那么每一维直接就是求距离的公式累加起来就可以了，最近的情况下面，则是如果处于最大最小区间以内，则是不用加，否则这一维取最小的来

​ 用图片来表示的话，大概就是这样

p1.PNG
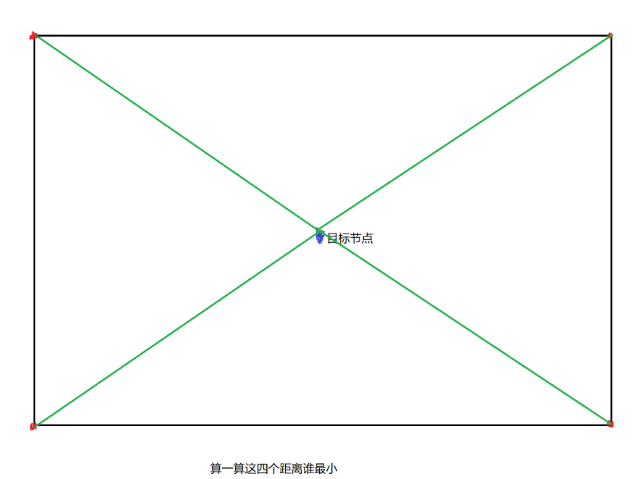
k2.png

上面的图就分别对应了第$k$近和第$k$远了

1
2
3
4
5
6
7
8
inline double getrange(int p,int pos){
	double res=0;
	if(Minp(pos,0)>D(p,0))res+=sqar(Minp(pos,0)-D(p,0));
	if(Maxp(pos,0)<D(p,0))res+=sqar(Maxp(pos,0)-D(p,0));
	if(Minp(pos,1)>D(p,1))res+=sqar(Minp(pos,1)-D(p,1));
	if(Maxp(pos,1)<D(p,1))res+=sqar(Minp(pos,1)-D(p,1));
	return res;
}//第k近
1
2
3
4
5
6
inline ll disrange(node pos,int nowp){
	ll res=0;
	for(int i=0;i<maxk;i++)
		res+=max(sqar(pos.databank[i]-Minp(nowp,i)),sqar(pos.databank[i]-Maxp(nowp,i)));
	return res;
}

数据类型不一样是因为不是从同一道题目上摘下来的，不要在意

那么这样一来，查询的代码就差不多可以写出来了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void query(int L,int R,int p){
		if(L>R)return;
		int mid=(L+R)>>1;
		if(mid!=p){
			ll res=0;
			for(int i=0;i<maxk;i++)
				res+=sqar(D(mid,i)-D(p,i));
			if(res>que.top()){
				que.pop();
				que.push(res);
			}
		}	
		ll disl=0,disr=0;
		disl=range(p,lc[mid]);
		disr=range(p,rc[mid]);
		if(disl>disr){
			if(disl>que.top())query(L,mid-1,p);
			if(disr>que.top())query(mid+1,R,p);
		}
		else{
			if(disr>que.top())query(mid+1,R,p);
			if(disl>que.top())query(L,mid-1,p);
		}
	}

这里就只写贴一个查询第$k$远的了

K-D tree 的查询时间复杂度据说是 $\Theta(\sqrt N)$

但是在某一些情况下面，它的时间复杂度还是会退化到接近$\Theta(N)$来，比如说

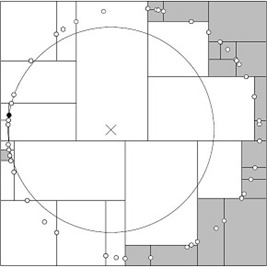
所有的节点分布大致构成了一个圆，而你查询的节点差不多就是在圆心位置。

当然，设节点数为$K$,维度为$D$,只有当$K >> 2^D$的时候，K-D tree的效率才可以保证，当然，维数如果说高了的话，效率也是无法保证的。想K-D tree这样可以解决多维信息的树还有别的，比如说球树等等，我就不说了。因为我不会用。而如果想要解决更高维的信息，还想要保证效率的话，那么还有一种方法

BBF 算法

​ 首先，我们需要另外一个优先队列。同时还需要一个对回溯次数限制的值，这个值是依据大量的结果取定的，我也不知道应该给你一个多少比较好。这个$BBF$算法的核心就在于决定一个优先级和最大回溯次数。这个优先级还是之前所说的距离来当。每一次查询到某一个节点的时候，还是计算出左右儿子和目标节点距离，然后进入其中一个查询，把另一个连同树上的位置和优先级一起放进优先队列里面来。然后查询一直到达叶子结点。如果队列不为空且没有到达最大回溯次数，那么就从队列里面拿出队首来进行查询。

插入，删除和重构

插入

这个时候，到达某一个节点，然后根据这个节点划分的维度，依次往下去，知道叶子节点为止，然后加上来就可以了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void insert(int now,node p,int deps){
	//插入操作，常规 
	keyd=deps%maxk;
	if(p.databank[keyd]<=D(now,keyd)){
		if(lc[now]==0){
			lc[now]=++tot;
			d[tot]=p;
		}
		else insert(lc[now],p,deps+1);
	}
	else{
		if(rc[now]==0){
		rc[now]=++tot;
		d[tot]=p;
		}
		else insert(rc[now],p,deps+1);
	}
	pushup(now);
}

差不多，就这样吧……

删除

K-D tree的删除操作，对于没有后继节点的节点，那么就直接删除了就好，但是如果说有后继节点的话，你就从它的左子树中，找出这一维最小的那一个值，或者是右子树中找出最大的那一个值，然后再把把那一个值从原来的树中删除了……这是一个递归实现的过程。

重构

当插入删除操作进行了一定次数以后，重新用一次$build$就好了。当然也可以类似替罪羊树那样，选择一个规定的$\alpha$，如果说不符合要求再使用一次$build$,不过我觉得还是一种方法更好

参考

oi-wiki

KD树（网易游戏笔试）

Kd-Tree算法原理和开源实现代码

K-D tree 数据结构

  1. 1. KNN问题
  2. 2. K-D tree
    1. 2.1. 概念
    2. 2.2. 建立
      1. 2.2.1. 解释
      2. 2.2.2. (假)代码
    3. 2.3. 查询
      1. 2.3.1. K-D tree 的K近邻查询
      2. 2.3.2. BBF 算法
    4. 2.4. 插入，删除和重构
      1. 2.4.1. 插入
      2. 2.4.2. 删除
      3. 2.4.3. 重构
  3. 3. 参考